Inverse Functions

An inverse function goes the other manner!

Permit usa start with an instance:

Here we have the role f(x) = 2x+3, written equally a flow diagram:

2x+3

The Inverse Role goes the other way:

Inverse

So the changed of:   2x+iii   is:   (y-3)/2

The changed is normally shown by putting a little "-1" after the function proper name, like this:

f-ane(y)

We say "f inverse of y"

So, the changed of f(10) = 2x+3 is written:

f-ane(y) = (y-3)/two

(I too used y instead of x to show that nosotros are using a different value.)

Back to Where Nosotros Started

The cool thing virtually the inverse is that it should give us back the original value:

banana f() to apple f()-inverse back to banana
When the function f turns the apple into a assistant,
Then the inverse part f-1 turns the banana back to the apple


Example:

Using the formulas from above, we tin start with x=four:

f(four) = ii×4+3 = 11

We can then use the inverse on the eleven:

f-1(11) = (11-three)/2 = 4

And nosotros magically get iv back once again!

Nosotros tin write that in one line:

f-i( f(4) ) = 4

"f changed of   f of 4   equals 4"

So applying a part f and then its changed f-one gives us the original value back once again:

f-i( f(x) ) = x

We could as well have put the functions in the other club and it still works:

f( f-ane(x) ) = 10

Instance:

Start with:

f-1(11) = (11-iii)/2 = four

And so:

f(iv) = 2×4+iii = 11

So we can say:

f( f-ane(xi) ) = xi

"f of   f changed of eleven   equals eleven"

Solve Using Algebra

Nosotros tin piece of work out the changed using Algebra. Put "y" for "f(x)" and solve for ten:

The function: f(x) = 2x+3
Put "y" for "f(x)": y = 2x+3
Subtract 3 from both sides: y-3 = 2x
Split both sides by 2: (y-3)/2 = ten
Swap sides: x = (y-3)/two
Solution (put "f-1(y)" for "ten") : f-1(y) = (y-3)/2

This method works well for more than hard inverses.

Fahrenheit to Celsius

A useful example is converting between Fahrenheit and Celsius:

To convert Fahrenheit to Celsius: f(F) = (F - 32) × five ix

The Inverse Part (Celsius back to Fahrenheit): f-ane(C) = (C × 9 v ) + 32

For you: see if you tin do the steps to create that inverse!

Inverses of Common Functions

It has been like shooting fish in a barrel so far, because nosotros know the inverse of Multiply is Split up, and the inverse of Add together is Subtract, but what near other functions?

Here is a listing to help y'all:

Inverses Careful!
add <=> Subtract
Multiply <=> Divide Don't split by zero
1 ten <=> 1 y x and y not aught
x2 <=> sqrt-y ten and y ≥ 0
xnorthward <=> nth-root-y or y^(1/n) north not zero
(different rules when due north is odd, even, negative or positive)
eastx <=> ln(y) y > 0
ax <=> loga(y) y and a > 0
sin(10) <=> sin-one(y) -π/two to +π/ii
cos(ten) <=> cos-1(y) 0 to π
tan(ten) <=> tan-1(y) -π/2 to +π/2

(Annotation: you tin read more about Inverse Sine, Cosine and Tangent.)

Conscientious!

Did you see the "Careful!" column above? That is because some inverses work only with certain values.

Example: Square and Square Root

When nosotros square a negative number, then do the changed, this happens:

Square: (−2)2 = 4

Inverse (Square Root): √(4) = 2

Only we didn't get the original value back! We got 2 instead of −two. Our fault for not being conscientious!

So the square function (equally it stands) does non have an inverse

But nosotros can ready that!

Restrict the Domain (the values that tin go into a function).

Example: (continued)

Just brand certain we don't use negative numbers.

In other words, restrict it to ten ≥ 0 and so nosotros tin can have an inverse.

So nosotros have this situation:

  • x2 does not have an inverse
  • but {x2 | x ≥ 0 } (which says "ten squared such that x is greater than or equal to naught" using set-builder notation) does accept an inverse.

No Inverse?

Let the states come across graphically what is going on here:

To be able to accept an inverse we need unique values.

Just think ... if there are ii or more than x-values for one y-value, how do we know which one to choose when going back?

Imagine we came from xi to a item y value, where exercise we get back to? 10one or 10two?

In that case nosotros can't have an inverse.

Simply if we can have exactly 1 ten for every y we can take an changed.

It is called a "one-to-i correspondence" or Bijective, like this

A function has to be "Bijective" to accept an changed.

So a bijective function follows stricter rules than a general function, which allows us to have an inverse.

Domain and Range

So what is all this talk near "Restricting the Domain"?

domain and range graph

In its simplest grade the domain is all the values that become into a office (and the range is all the values that come out).

As information technology stands the function higher up does not accept an inverse, considering some y-values volition have more than one x-value.

doman and range

But we could restrict the domain so there is a unique ten for every y ...

doman and range

... and now we can accept an inverse:

Note as well:

  • The role f(ten) goes from the domain to the range,
  • The inverse office f-1(y) goes from the range back to the domain.

Let's plot them both in terms of x ... so information technology is at present f-i(x), not f-1(y):

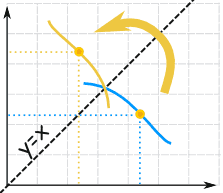
doman and range

f(x) and f-1(10) are similar mirror images
(flipped most the diagonal).

In other words:

The graph of f(ten) and f-one(x) are symmetric beyond the line y=ten

Example: Square and Square Root (continued)

Get-go, we restrict the Domain to x ≥ 0:

  • {x2 | x ≥ 0 } "10 squared such that 10 is greater than or equal to zero"
  • {√x | x ≥ 0 } "square root of x such that x is greater than or equal to null"

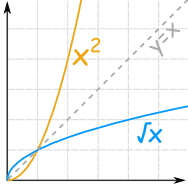
x^2 vs square root x
And you lot can see they are "mirror images"
of each other near the diagonal y=10.

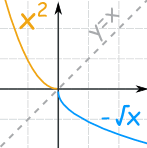
x^2 vs -square root x

Note: when we restrict the domain to 10 ≤ 0 (less than or equal to 0) the inverse is and so f-1(x) = −√10:

  • {x2 | ten ≤ 0 }
  • {−√ten | x ≥ 0 }

Which are inverses, besides.

Not Always Solvable!

It is sometimes not possible to notice an Inverse of a Role.

Example: f(ten) = 10/2 + sin(x)

We cannot work out the changed of this, because we cannot solve for "x":

y = ten/2 + sin(x)

y ... ? = x

Notes on Notation

Even though we write f-1(x), the "-one" is not an exponent (or power):

f-1(x) ...is different to... f(x) -1
Inverse of the part f f(x)-i = 1/f(10)
(the Reciprocal)

Summary

  • The inverse of f(x) is f-one(y)
  • We tin can discover an changed by reversing the "flow diagram"
  • Or nosotros can observe an inverse past using Algebra:
    • Put "y" for "f(ten)", and
    • Solve for ten
  • We may need to restrict the domain for the function to accept an inverse